Bayesian A/B Testing
And how it compares to the Frequentist approach
What is an A/B test?
A/B testing is a technique to compare two treatments.
Example: we made a new landing page for our website. We would like to know: does the new page make more people sign up? In A/B testing we answer this question by showing the current page to the first group of users A, and the new page to another group of users B. We calculate the conversion rates and use statistical methods to decide whether the effect we observe is significant or due to chance.
Traditionally an A/B test is performed using frequentist methods. However, a contender is gaining popularity: Bayesian A/B testing. In this article, I will give a brief intro to A/B testing and compare both approaches, focusing on Bayesian one.
If you are already familiar with Frequentist A/B testing you scroll go straight to the Bayesian part.
Frequentist A/B testing
The algorithm to perform a traditional A/B test is the following:
Formulate the hypothesis.
The null hypothesis is that there is no significant change. We will collect data and see if it’s possible to reject it. If the data demonstrate that the hypothesis is wrong we reject it and conclude that the observed changes are significant.
The null hypothesis:
The alternative hypothesis is that group B has a significantly different conversion rate.
Design the experiment
Choose a metric that we will be comparing. In our case of website page comparison, the metric will be Click Through Probability: the probability of pressing the sign-up button.
Assume a probabilistic model for the process. In our case, we will assume that each user can either sign up or not, so we treat them as a Bernoulli trial. The probability follows the Binomial distribution.
Estimate the required sample size and length of the experiment. This requires picking three values: alpha, beta, delta.
One of the ways to compute sample size:
Scary thing, right? I have something scarier: this is just one way to estimate the required sample size. You can find others, for example here, here, and here. To be honest I am not sure which one is correct and how to choose between them. Your best bet is to use a sample size calculator.
Alpha is the probability of rejecting the null hypothesis when it should not be rejected. It’s known as the significance level or Type I error rate. A common value is 0.05.
Beta is the probability of failing to reject the null hypothesis when it should be rejected. For example, concluding that conversion is the same for two pages, while actually one of the variants is better. This is known as the false negative rate or Type II error rate. A typical value for beta is 0.2.
How do we choose alpha and beta? It’s a balance between how much resources we can allocate for the test and how sure we want to be of our results. Everyone ended up agreeing on an arbitrary standard: alpha = 0.05, beta = 0.2.
Delta is the minimum detectable effect: what kind of conversion change we would accept to be worth the trouble of running the experiment? One example could be 0.01, which means we are looking for at least a 1% increase in conversion.
We also need p_bar and q_bar, which can be obtained using A/A testing (an A/B test where we show the same page to both groups).
Run the experiment
Split users into groups A and B. The groups must not overlap. Then perform the experiment until the desired sample size is obtained.
Perform a statistical test
We need to perform a test that will tell us: is the observed difference significant?
There are three ways to perform such a test:
Compute a test statistic and a p-value for it. In this case a test for sample means.
Obtain confidence intervals for the metric and compare them.
Apply a regression model.
Let’s focus on the first approach. We will use the 2-sample Z-test for the equality of sample means.
First, compute the conversion rates as sample means:
We are testing for the difference in these probabilities.
Compute the pooled probability, and estimate the pooled variance and standard error:
Compute the test statistic of the 2-sample Z-test:
Compute the p-value:
What p-value means: if we ran an A/A test with the same sample size, the probability of seeing the result at least as “extreme” as what we saw is smaller than p-value. To compute the p-value we look up the test statistic probability in a table or using a statistical package.
Don’t worry if it seems convoluted to you because it is convoluted for everyone.
Analyze the results
Given confidence intervals we have two cases:
If p-value is smaller than alpha, our confidence threshold, we reject the Null hypothesis and assume there is a significant difference between the means. We conclude that the new page performs better or worse.
If p-value is bigger than alpha, we fail to reject the Null hypothesis and conclude the new landing page does not make a difference.
Issues with the Frequentist Approach
1. Does not answer the questions we need
People are really interested in this question: does the B version of the web page perform better than A? They would like to know1:
Yet the classic A/B test can not answer this question. Instead, it can compute a p-value.
If you take the confidence interval route, you also get something different from what you want:
Once you’ve calculated a confidence interval, it’s incorrect to say that it covers the true mean with a probability of 95% (this is a common misinterpretation). You can only say, in advance, that in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean.2
2. Alpha and beta are arbitrary
The choice of these parameters heavily impacts the result.
3. You can only analyze results after the experiment ran
It’s not uncommon to run the whole experiment only to find out that the results are inconclusive. This might be costly in real life. Imagine being a scientist that spent a year observing patients in two groups only to find out there is no result to show because the experiment should have been run for longer.
4. The test is not valid if assumptions are violated
And oh boy there are so many assumptions.
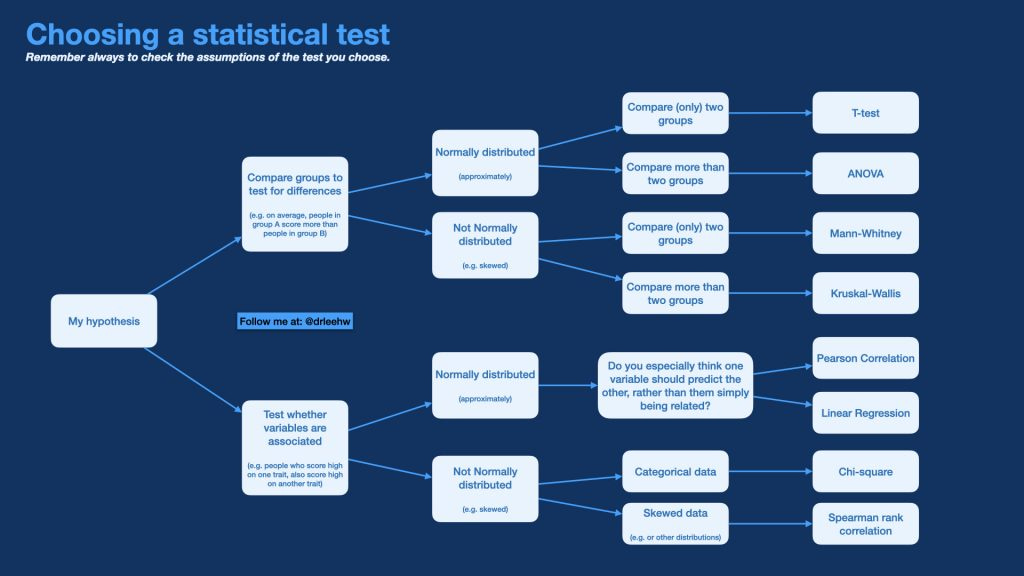
Just take a look at a cheatsheet for choosing the right statistical test3:
Bayesian statistics ELI5
You lost your phone somewhere in the house. You hear a buzz from somewhere. If you follow the frequentist approach, the buzz is all the data you have. If you are Bayesian, then you also have your memories about where you were using your phone and guesses about where the phone might end up.
Another example: you are waiting for a bus at a bus stop. You see the bus turning the corner. What is the probability that the bus arrives within three minutes? Frequentist says: it’s a Poisson process blah blah blah. Bayesian says: I can see the damn bus, the probability is approaching one.
You could say Bayesian statistics is a way to incorporate assumptions and prior knowledge into statistical inference. The Bayesian way says that probability is not the frequency of some event but a measure of subjective uncertainty. Therefore in Bayes, everything is a random variable. Each parameter is a random variable and its distribution represents our beliefs and knowledge about its values.
It bends your mind a bit.
Bayesian approach to A/B testing
Assume each user shown A has probability lambda_A to convert. Same for group B and lambda_B. We want to know the distribution of parameters lambda_A and lambda_B. If knew that we would be able to answer questions like “how likely it is that conversions are better in group B?” In math lingo:
We run an A/B test and gather data. We want to use it to infer P(lambda | data).
Bayes rule will help, for example for group A:
We just turned the conditional probability around.
Examine the terms:
p(data|lambda) — likelihood, i.e. how likely it is to observe such data for some select value of the parameter.
p(lambda) — prior. This one is tricky. We have to choose this prior as some distribution that represents our beliefs about what lambda might look like.
p(data) — the probability to observe this sample no matter what the parameters are. It’s a constant actually. It normalizes the nominator to fall between 0 and 1, to make it a valid probability distribution. You can get this constant if you integrate the nominator, but it’s usually a pain.
The process works like this: we take our prior belief p(lambda), observe some data, compute likelihood and likelihood “moves” our belief by multiplying the prior. The result, p(lambda|data) is called posterior. This is what we believe after we have adjusted our prior beliefs for the data we observed.
Choosing a model
On the Bayesian path, we have to make our idea about how the problem works explicitly by defining the probabilistic model. I will go with the following: groups A and B have conversion rates sampled from some distribution, for example, Beta (more on that later). Then each user tosses an unfair coin to decide whether to convert. So each user is a Bernoulli trial with a probability equal to the conversion rate.
Here’s my model pictured:
Maybe users are not tossing coins, I have no idea. But my model does not need to be perfect, it just has to reflect reality enough, and I can improve it later.
Choosing a prior
If I don’t know anything about conversions I can choose this prior, Beta(1, 1):
This is a fine prior that says that all conversions are equally likely. It will take little evidence to “change my mind” by adjusting it with data.
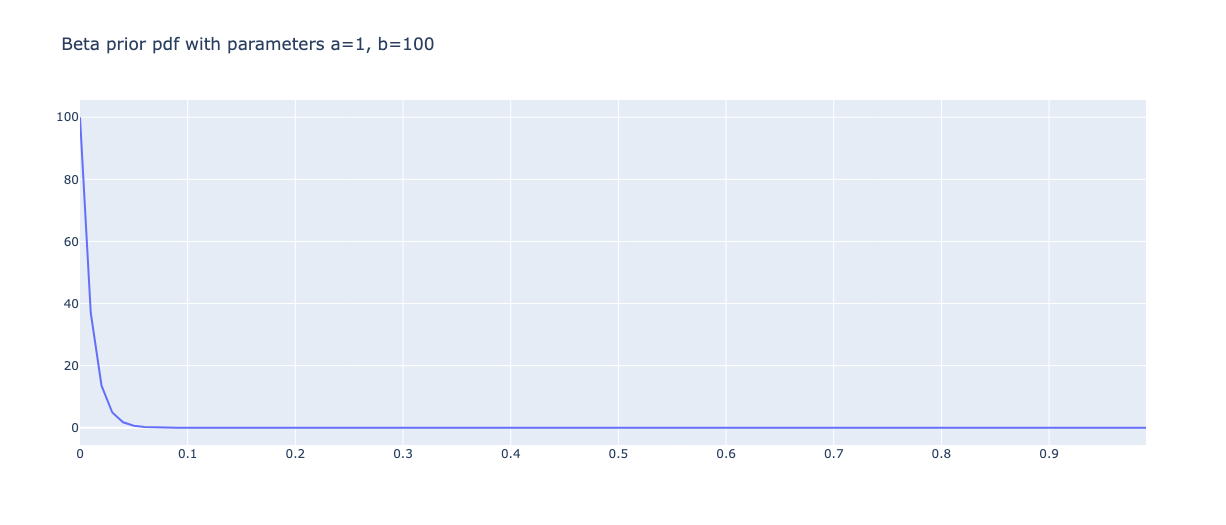
However, I know conversions are usually small, so I will go with this prior, Beta(1, 100):
This is essentially me assuming on average 1 in 100 people convert.
There is no right way to choose a prior. Lucky for us it does not matter as much as long as you don’t make it absurdly extreme and have enough data to change your mind.
Estimating the posterior
Finally, having defined a model and chosen a prior we generate data by running the experiment. We show variation A to N_A people and count how many users converted C_A. Same for B.
In our specific case, the posterior can be calculated analytically. But we will take an easier path than taking some integrals: just compute stuff.
To estimate the posterior we can just simulate the whole process. First, sample some conversion rate from the prior. Compute the likelihood to observe our data with this conversion rate. Multiply. Bam, that’s one data point for our posterior. Do this ten thousand times for each group and we will have a good approximation of our posterior.
Thank God we don’t need to do it by hand, Python plus PyMC takes does the heavy lifting of sampling for us:
import pymc as pm
import arviz as az
n_samples = 200
true_p_a = 0.05
true_p_b = 0.05
data_A = np.random.binomial(1, true_p_a, size=n_samples)
data_B = np.random.binomial(1, true_p_b, size=n_samples)
print('Sample means:')
print(f'Blue: {data_A.mean():.3%}')
print(f'Red: {data_B.mean():.3%}')
prior_alpha = [5, 5]
prior_beta = [100, 100]
with pm.Model() as model:
A_rate = pm.Beta('A_conversion', prior_alpha[0], prior_beta[0])
B_rate = pm.Beta('B_conversion', prior_alpha[1], prior_beta[1])
A_obs = pm.Bernoulli('A_observations', A_rate, observed=data_A)
B_obs = pm.Bernoulli('B_observations', B_rate, observed=data_B)
trace = pm.sample(return_inferencedata=True)
az.plot_posterior(trace)And this is what we get:
On the left is a plot of the approximated posterior for group A. On the x axis we have conversion rates, on the y axis how probable they are. It says the conversion rate is between 0.03 and 0.075 with probability 0.94. Notice how this is not some convoluted confidence interval. This is a credible interval and it tells us exactly what we need to know.
In this example the true conversion rates are the same, so the credible interval is very similar.
If the true rates were different we could see:
The credible intervals overlap. But we are not in some yes-or-no world of frequentist A/B testing, so we won’t conclude anything based on just that. Instead, we can estimate: how likely it is that B conversions are actually better than A?
samples_A = trace.posterior['A_conversion'].values
samples_B = trace.posterior['B_conversion'].values
print(f'Probability that B is better: {(samples_B > samples_A).mean():.1%}.')
# Probability that B is better: 95.7%.Now we can make our decision. Is 4.3% probability of being wrong too much for us? Depends on our situation.
Conclusion
We have taken a look at classic A/B testing and introduced Bayesian A/B testing. The Bayesian approach to this problem provides an intuitive, simple yet effective framework.
https://vwo.com/downloads/VWO_SmartStats_technical_whitepaper.pdf
https://www.probabilisticworld.com/frequentist-bayesian-approaches-inferential-statistics/
https://leehw.com/crib-sheets/statistical-test-cheat-sheet/






Thank you for the post! Please explain source code where 95.7% got. What values do we compare here?